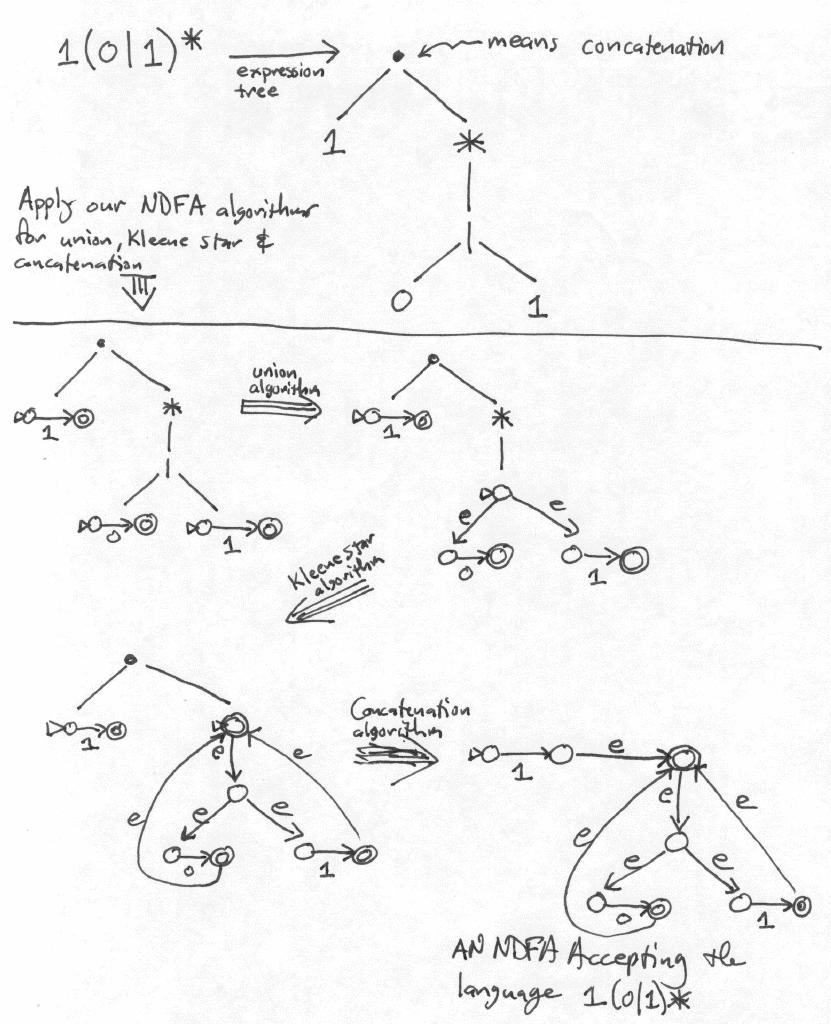
A quick overview of RegEx

Regular Expressions (RegEx) are a very common tool in computer science, often used for search-and-replace operations, finding specific strings or patterns in large files, and validating user input (see the infamous email regex).

In introductory classes to theoretical computer science, we see regular expressions as an example application of automata theory, more precisely finite automata. The process of converting a RegEx into an automaton is called Thompson's construction, and is behind grep's unreal speed.

The problem at hand

When building Proposition 7, I was struggling with a very peculiar problem in program synthesis and input validation.

Correctness by complete-ability

The p7 expression parser is based on a very simple principle:

With $\Sigma$ an alphabet and $L$ a language, we can define a function

\Phi : \Sigma^* \rightarrow \{\text{accept},\text{reject}\}

as follows:

\Phi(s) = \begin{cases} \text{accept} & \exists s' \in \Sigma^*,\, ss' \in L \\ \text{reject} & \text{otherwise} \end{cases}

Our goal here, for constrained generation, is to ensure that any prefix $s$ of a valid expression can be completed into a valid expression in $L$ and thus lead to a valid program of proof.

RegEx sub-problem

Since our language $L$ is defined by complex mechanisms, such as typing rules and recursive grammars, it must be handled by a Turing-complete model in the general case. However, a subset of this problem requires a generalized solution for RegEx.

Consider the following grammar as an example:

expr ::= /b(u|o|i)p/
term ::= expr ('and' expr)* 
prog ::= term 'at' 'bap'

expressions between slashes (/<regex>/) are regexes

The program bip at bap is a trivial valid expression, as is bip and bop at bap. However, bip and is not a valid expression, but can be completed into one by adding another expr + at bap after the and. We can call it $\Sigma\text{-completeable}$ in $L$ .

Now, consider that we are working with a system that produces output byte by byte. How can we validate the expression bi or bip an? Both are prefixes of completeable expressions, but neither is a $\Sigma\text{-completeable}$ expression.

Formally, we could say that our grammar defines a language $L$ over an alphabet $\Sigma = \{ \text{/b(u|o|i)p/}, \text{'and'}, \text{'('}, \text{')'}, \text{'at'}, \text{'bap'} \}$ and that this alphabet is itself a language $L_\Sigma$ over the alphabet of bytes $\Sigma_{\text{byte}} = [0..255]$ (or more generally $\Sigma_\text{vocab}$ corresponding to any vocabulary where $\Sigma_\text{vocab} \subseteq \Sigma_{\text{byte}}^*$ and $\Sigma \subseteq \Sigma_\text{vocab}^*$ ).

Disambiguation of $L_\Sigma$

$L_\Sigma$ can be decomposed as the union of all keywords in $\Sigma$ . Each element $l \in \Sigma$ defines a language $L_l \subseteq \Sigma_\text{vocab}^*$ , where $L_l$ is either a singleton set (for fixed keywords) or a regular language (for patterns like identifiers)¹:

L_\Sigma = \bigcup_{l\in \Sigma} L_l

For example, in our grammar:

$L_{\text{'and'}} = \{\text{'and'}\}$ (a fixed keyword)
$L_{\text{/b(u|o|i)p/}} = \{\text{'bup'}, \text{'bop'}, \text{'bip'}\}$ (a regex pattern)

Each $L_l$ can be represented by a regular expression $r_l$ such that $L(r_l) = L_l$ . Therefore:

L_\Sigma = \bigcup_{l\in \Sigma} L(r_l)

Following this, we can define $r_\Sigma = \bigcup_{l \in \Sigma} r_l$ such that $L(r_\Sigma) = L_\Sigma$

Validation from $\Sigma_\text{vocab}$ to $L_\Sigma$

To validate partial inputs over $\Sigma_\text{vocab}$ , we can define a function

\pi(s) : \Sigma_{\text{vocab}}^* \rightarrow \{\text{complete},\text{partial},\text{reject}\}

as follows:

\pi(s) = \begin{cases} \text{complete} & s \in L_\Sigma \\ \text{partial} & s \notin L_\Sigma \land \exists s' \in \Sigma_{\text{vocab}}^*,\, ss' \in L_\Sigma \\ \text{reject} & \text{otherwise} \end{cases}

This function bridges the gap between the formal language's alphabet and the model vocabulary, allowing us to validate all possible partial (complete-able) inputs.

$\Sigma_{\text{vocab}}\text{-completeability}$ in $L$

Now that we have a function relating our model's vocabulary $\Sigma_\text{vocab}$ to the formal language's alphabet $\Sigma$ , we can define a function that directly relates the model's vocabulary to the completeability in $L$ noted $\hat{\Phi}$ :

\hat{\Phi}: \Sigma_{\text{vocab}}^* \rightarrow \{\text{accept},\text{reject}\}

Let $t_1 \cdots t_n \cdot t'$ be a tokenization of input $s \in \Sigma_{\text{vocab}}^*$ where $t_1, \ldots, t_n \in \Sigma$ are complete tokens and $t' \in \Sigma_{\text{vocab}}^*$ is the remaining partial input (noted $\varepsilon$ if empty).

\hat{\Phi}(s) = \begin{cases} \text{accept} & t' = \varepsilon \land \Phi(t_1 \cdots t_n) = \text{accept} \\ \text{accept} & t' \neq \varepsilon \land \pi(t') = \text{partial} \land (\exists q \in \Sigma_{\text{vocab}}^*, t'q \in L_\Sigma, \Phi(t_1 \cdots t_{n}(t' q)) = \text{accept})\\ \text{reject} & \text{otherwise} \end{cases}

For disambiguation see²

This captures that we accept a partial input if either

It fully tokenizes into element of $\Sigma$ and parses correctly in $L$
The partial token $t'$ can be completed by some $q \in \Sigma_{\text{vocab}}^*$ into a valid token $l \in \Sigma$ such that and appending $l$ to the complete tokens yields an expression that is $\Sigma\text{-completeable}$ in $L$ .

Keeping with our example, bi and bip an are both $\Sigma_{\text{vocab}}\text{-completeable}$ in $L$ , as they can be completed into valid expressions in $L_\Sigma$ : bip and bip and that are themselves $\Sigma\text{-completeable}$ in $L$ . On the other hand, bip at bo is not $\Sigma_{\text{vocab}}\text{-completeable}$ in $L$ , because while it can be completed into the $L_\Sigma$ expression bip at bop, this expression is not $\Sigma\text{-completeable}$ in $L$ (it is even outright invalid).

Implementation

Focusing on the regex aspect of the program, we want to implement $\pi(s)$ for the case where $L_\Sigma$ is defined by a regex $r_\Sigma$ . We cannot trivially do this by directly manipulating automata, but need a more general mechanism on the expressions themselves. In short, we need something that can tell us if a string $s \in \Sigma_{\text{vocab}}^*$ is a valid prefix of a string in $L_\Sigma$ .

One approach is find the set of suffixes $S = \{ s' \in \Sigma_{\text{vocab}}^* \mid ss' \in L_\Sigma \}$ , and check if $S$ is non-empty. The completing suffix of $s$ is known as the quotient of $L_\Sigma$ with respect to $s$ , and is written $s^{-1}L_\Sigma$ . The expression that can produce this set of quotients is known as the Brzozowski derivative of $L_\Sigma$ with respect to $s$ , and is written $D_s(L_\Sigma)$ .

We work with a standard regular-expression syntax over the alphabet $\Sigma_{\text{vocab}}$ to define $L_\Sigma$ :

$\emptyset$ (empty language), $\varepsilon$ (empty word)
literals $a \in \Sigma_{\text{vocab}}$ and character ranges $[a..b] = \{ x \in \Sigma_{\text{vocab}} \mid a \le x \le b \}$
union $r + s$ , concatenation $rs$ and Kleene star $r^*$

Let $L(r) \subseteq \Sigma_{\text{vocab}}^*$ denote the language of regex $r$ , so that $L_\Sigma = L(r_\Sigma)$ for some regex $r_\Sigma$ . The (left) quotient of a language by a character $c \in \Sigma_{\text{vocab}}$ is

c^{-1}L \;=\; \{ w \in \Sigma_{\text{vocab}}^* \mid cw \in L \}.

We also introduce $\nu(r)$ ("nullable") as the predicate that holds exactly when $\varepsilon \in L(r)$ :

$\nu(\emptyset) = \text{false}$
$\nu(\varepsilon) = \text{true}$
$\nu(a) = \text{false}$
$\nu([a..b]) = \text{false}$
$\nu(r + s) = \nu(r) \lor \nu(s)$
$\nu(rs) = \nu(r) \land \nu(s)$
$\nu(r^*) = \text{true}$

We can then define our Brzozowski derivative ( with $c \in \Sigma_{\text{vocab}}~$ ):

\begin{aligned} D_c(\emptyset) &= \emptyset \\ D_c(\varepsilon) &= \emptyset \\ D_c(a) &= \begin{cases} \varepsilon & \text{if } a = c \\ \emptyset & \text{otherwise} \end{cases} \\ D_c([a..b]) &= \begin{cases} \varepsilon & \text{if } a \le c \le b \\ \emptyset & \text{otherwise} \end{cases} \\ D_c(r + s) &= D_c(r) + D_c(s) \\ D_c(r\cdot s) &= D_c(r)\cdot s \;\cup\; \begin{cases} D_c(s) & \text{if } \nu(r) \\ \emptyset & \text{otherwise} \end{cases} \\ D_c(r^*) &= D_c(r)\cdot r^* \end{aligned}

We can then extend the derivative to arbitrary strings by left-folding on characters (over $\Sigma_{\text{vocab}}$ ):

\begin{aligned} D_{\varepsilon}(r) &= r, \\ D_{xc}(r) &= D_c\bigl(D_x(r)\bigr), \quad x \in \Sigma_{\text{vocab}}^*,\; c \in \Sigma_{\text{vocab}}. \end{aligned}

Equivalently, we apply recursively for $s = c_1 c_2 \cdots c_n \in \Sigma_{\text{vocab}}^*$ ,

D_s(r) = D_{c_n}\bigl(\cdots D_{c_2}(D_{c_1}(r))\cdots\bigr).

Correctness connects completion to nullability. For the keyword-recognizing regex $r_\Sigma$ (where $L(r_\Sigma) = L_\Sigma$ ):

ss'\in L(r)\iff s'\in L(D_s​(r)).

This is precisely the test we need for complete-ability in $\pi$ : given a partial input $s \in \Sigma_{\text{vocab}}^*$ , compute $D_s(r_\Sigma)$ and check $D_s(r_\Sigma) = \emptyset$ :

\pi(s) = \begin{cases} \text{complete} & \nu(D_s(r_\Sigma)) \\ \text{partial} & D_s(r_\Sigma) \neq \emptyset \\ \text{reject} & \text{otherwise} \end{cases}

cases evaluated in order for disambiguation

Correspondence to code

The Rust definition below implements $D_c$ and then folds it over a string $s$ :

fn char_derivative(&self, c: char) -> Regex {
    use Regex::*;
    match self {
        Empty => Empty,
        Epsilon => Empty,
        Char(ch) => if *ch == c { Epsilon } else { Empty },
        Range(start, end) => if *start <= c && c <= *end { Epsilon } else { Empty },
        Union(a, b) => Union(Box::new((**a).char_derivative(c)), Box::new((**b).char_derivative(c))),
        Concat(a, b) => {
            let da = a.char_derivative(c);
            if a.nullable() {
                Union(
                    Box::new(Concat(Box::new(da), Box::new((**b).clone()))),
                    Box::new(b.char_derivative(c)),
                )
            } else {
                Concat(Box::new(da), Box::new((**b).clone()))
            }
        }
        Star(r) => Concat(Box::new((**r).char_derivative(c)), Box::new(Star(r.clone()))),
    }
}

pub fn derivative(&self, s: &str) -> Regex {
    s.chars().fold(self.clone(), |acc, c| acc.char_derivative(c))
}

In practice, one also applies algebraic simplifications after each construction (e.g., $\emptyset + r = r$ , $\emptyset r = \emptyset$ , $\varepsilon r = r$ ) to control expression growth.

In the real implementation, we use the Brzozowski derivative not only to implement $\pi(s)$ , but also as a policy for the sampling system in the constrained decoding core of Proposition 7.

Conclusion

In a real world implementaiton with grammar defined in EBNF-like format and an input $s$ over $\Sigma_\text{vocab}$ , we can implement $\hat{\Phi}(s)$ as follows:

Tokenize $s$ into tokens $t_1, t_2, \ldots, t_n$ over $\Sigma$ .

If tokenization succeeds and $s$ is fully tokenized, return $\Phi(s)$
If tokenization fails with remaning input $t'$ , continue to step 2

Compute $r' = D_{t'}(r_\Sigma)$ where $r_\Sigma = \sum_{l \in \Sigma} r_l$
Build the set $T_{n+1} = \{y \in \Sigma | ~\exists (t_{n+2},t_{n+3},...t_{n+k}) \in \Sigma^*, \Phi(t_1t_2...t_n~y~t_{n+2},t_{n+3},...t_{n+k}) = \text{accept}\}$ of possible next continuations in $L$
Check if $\exists x \in \Sigma_\text{vocab}^*,l \in \Sigma$ such that $\exists \tau \in T_{n+1}, \tau = l~x$ where $\nu(D_{t'x}(r_l)) = \text{true}$.
- If yes, return accept
- Otherwise, return reject

For the precise use case of constrained generation, $T_{n+1}$ and $r'$ are passed to the sampling system and applied as filters on the model's vocabulary $\Sigma_\text{vocab}$ to only allow tokens that can complete $s$ into a valid expression.

Obviously, this is only a small piece in the puzzle, and a lot of challenges remain with the implementation of $\Phi$ on arbitrary, context-dependent, languages, with context and type dependencies. It's still cool to see how basic concepts like this have deep implications and practical value in real-world systems.

For the purposes of this article, we assume tokenization follows the longest match principle: when multiple tokens could match a prefix of the input, the longest matching token is selected. This ensures deterministic tokenization and prevents ambiguity in the decomposition above. For instance, if both 'a' and 'and' are in $\Sigma$ , the input "and" tokenizes uniquely as the token 'and' rather than 'a' followed by remaining input "nd".

Since $\pi(t') = \text{partial}$ guarantees that some completion of $t'$ exists, the second case checks whether at least one such completion (noted here $t'q$ ) validates the $\Phi$ condition and yields a $\Sigma$ -completeable expression. For constrained sampling, finding any valid path forward suffices.

Completeability and Regular Expressions